Floating-Point Performance
Characterization of PowerPC 440 CPU using Fractal
Sets
Overview
Features
Hardware Architecture
Clocking
Infrastructure
Glossary
Fractal Kernels
Basic Kernel
Dual-Issue
Kernel
Implementation Results
Performance Assessment
Julia Set
Mandelbrot
Set
Summary & Conclusions
Outlook
References
This project briefly describes the implementation of a fractal compute kernel on a FPGA prototyping platform with an embedded PowerPC 440 CPU and floating-point coprocessor, including visualization of the fractal set on an external TFT display. The main objectives of this project are summarized as follows:
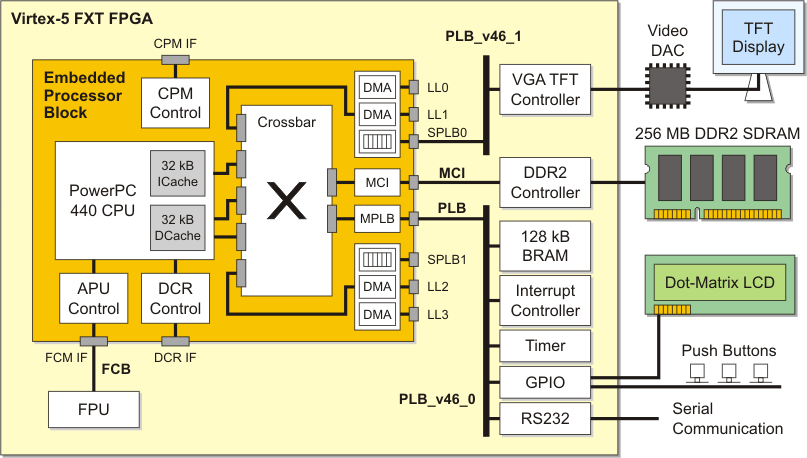
The hardware architecture consists of:
The hardware architecture is depicted below. Besides the TFT display and the serial communication, all components are part of the Xilinx ML507 FPGA prototyping board.
 |
| Hardware architecture for the fractal project. Visual output is accomplished through the VGA TFT controller and the TFT display. User control is realized through serial communication and push buttons. The VGA TFT controller implements a PLB master device, which is capable of performing autonomous data transfers from its assigned video memory, in this case a section of the DDR2 SDRAM. In this context, it is important to note that the PowerPC CPU needs to perform a cache flush of the video data once it is completely computed and ready to be displayed. |
The clocking scheme of the system architecture needs to adhere
to a bunch of different rules imposed by various interconnect and
device specifics. The applied clocking scheme and the
corresponding important clock ratios are listed below.
| Clock | Frequency | Clock Ratio |
| CPU core clock | 400 MHz | |
| FCM clock (APU) | 200 MHz | CPU:FCM 2:1 |
| CPM clock | 200 MHz | CPU:CPM 2:1 |
| MCI | 200 MHz | CPM:MCI 1:1 |
| DDR2 | 200 MHz | MCI:MEM 1:1 |
| MPLB (PLB_v46_0) | 100 MHz | CPU:MPLB 4:1, CPM:MPLB 2:1 |
| SPLB0 (PLB_v46_1) | 200 MHz | CPU:SPLB 2:1, CPM:SPLB0 1:1 |
| TFT | 25 MHz |
| APU | Auxiliary Processing Unit |
| BRAM | Block Random Access Memory |
| CPM | Communications Processor Module |
| DAC | Digital-to-Analog Converter |
| DCR | Device Control Register |
| DMA | Direct Memory Access |
| FCB | Fabric Coprocessor Bus |
| FCM | Fabric Coprocessor Module |
| FPU | Floating-Point Unit |
| GPIO | General Purpose Input/Output |
| MCI | Memory Controller Interface |
| MPLB | Processor Local Bus Master |
| SPLB | Processor Local Bus Slave |
| PLB | Processor Local Bus |
| PPC | PowerPC |
The initial kernel for computing the fractal sets has been
written in plain C using floating-point arithmetics. For each
data point (pixel) in the complex-valued coordinate system, the
basic fractal kernel computes:
iter = 0; |
This kernel contains the following (dominant) floating-point
operations:
|
|
|
Here, I only focus on add/sub, multiply and compare operations
and intentionally neglect any load/store instructions. According
to the FPU data sheet, the add/sub operation requires 5 (6) clock
cycles, the multiplication 4 (6) clock cycles, and the compare
operation 4 (4) clock cycles in single- (double-) precision data
format for the 200 MHz high-speed FPU variant. Moreover, the
FPU coprocessor is specified to be fully pipelined for add/sub
and multiply operations, and incorporates 32 floating-point
registers.
In the end, the fractal kernel exhibits 9 dominant floating-point
operations (FLOPS) per iteration, a fact that is used in the
subsequent performance analysis.
A fruitful attempt to improve the computational performance
has been made by extending the basic fractal kernel to a
dual-issue variant. In other words, the revised fractal kernel
computes now two independent (adjacent) pixels per loop
iteration, and thus improves the computational performance based
on the following rationale:
| Temporal Locality: | The data required for processing is still present in the data cache and/or the CPU/FPU registers. No extra load/store operations are required. |
| Spatial Locality: | The data required for processing is accessed through one or several contiguous memory access operations and is cached in the corresponding cache locations. In general, sequential access on contiguous data is superior to random access. |
| Data Dependency: | i) Identical operations on the same data
can be fused, e.g., the twofold occurrence of zr*zr (or
zi*zi) in the code example above are merged by the C
compiler into a single operation and the corresponding
intermediate result is re-used. ii) Independent data can be interleaved in order to increase the computational load on certain processing blocks. As such, a certain degree of concurrency in data processing might increase the aggregated computational throughput. Nevertheless, the applicable degree of concurrency depends on the individual CPU/coprocessor architecture, e.g., the amount of CPU/FPU registers, support for multiple pipelined instructions, and the cache architecture. Therefore, successful application of concurrency requires careful software adaptations in order to achieve increased aggregated computational performance. |
In short, the main goal of the dual-issue fractal kernel is to increase the average load on the FPU by exploiting its support for pipelined instructions. This goal is ultimately motivated by the fundamental guiding principle 'Make the common case fast!'.
The implementation of the dual-issue fractal kernel finally looks like:
iter0 = 0; |
Further experiments with a triple-issue fractal kernel showed a decrease in overall performance.
Please note, that the above code examples allow variable iter to be in range [0, max_iter+1], depending on the individual abort condition.
 |
 |
|
| Mandelbrot set computed on the Xilinx ML507 prototyping platform. | Mandelbrot set at increased zoom level. |
Using VGA resolution, the fractal image computation involves a
total of 307'200 pixels. Each pixel represents a complex-valued
number consisting of two single- or double-precision
floating-point values, i.e., in total 8 or 16 bytes per pixel.
The total computation time per image is showed for two selected
Julia and Mandelbrot sets in the corresponding tables
below.
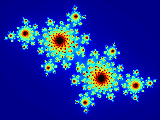 |
Parameters: c = -0.4 + 0.6i x_origin = -1.4400 y_origin = -1.0800 resolution = 0.0045 max_iter = 130 dimensions = 640x480 pixels |
average number of iterations per pixel = 21.3
| FPU coprocessor | not present | single-precision FPU | double-precision FPU | |
| data format | single-precision | double-precision | single-precision | double-precision |
| basic kernel | 20.185s | 30.839s | 1.248s | 1.416s |
| dual-issue kernel | 20.835s | 31.321s | 0.944s | 1.007s |
| performance gain | -3.2 % | -1.6 % | 24.4 % | 28.9 % |
Since we have previously identified the dominant
floating-point operations per iteration of the fractal kernel,
i.e., 9 FLOPS per iteration, the corresponding floating-point
performance can be calculated based on the following
parameters:
| pixels per image | 307'200 |
| average iterations per pixel | 21.3 |
| FLOPS per iteration | 9 |
| FPU coprocessor | not present | single-precision FPU | double-precision FPU | |
| data format | single-precision | double-precision | single-precision | double-precision |
| basic kernel | 2'918'000 | 1'910'000 | 47'188'000 | 41'589'000 |
| dual-issue kernel | 2'827'000 | 1'880'000 | 62'384'000 | 58'481'000 |
| performance gain | -3.2 % | -1.6 % | 24.4 % | 28.9 % |
Numbers represent FLOPS.
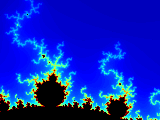 |
Parameters: c = 0 x_origin = -1.0600 y_origin = 0.2350 resolution = 0.0003 max_iter = 120 dimensions = 640x480 pixels |
average number of iterations per pixel = 33.2
| FPU coprocessor | not present | single-precision FPU | double-precision FPU | |
| data format | single-precision | double-precision | single-precision | double-precision |
| basic kernel | 30.985s | 47.417s | 1.898s | 2.171s |
| dual-issue kernel | 31.761s | 47.752s | 1.426s | 1.510s |
| performance gain | -2.5 % | -0.7 % | 24.9 % | 30.4 % |
Since we have previously identified the dominant
floating-point operations per iteration of the fractal kernel,
i.e., 9 FLOPS per iteration, the corresponding floating-point
performance can be calculated based on the following
parameters:
| pixels per image | 307'200 |
| average iterations per pixel | 33.2 |
| FLOPS per iteration | 9 |
| FPU coprocessor | not present | single-precision FPU | double-precision FPU | |
| data format | single-precision | double-precision | single-precision | double-precision |
| basic kernel | 2'962'000 | 1'936'000 | 48'362'000 | 42'281'000 |
| dual-issue kernel | 2'890'000 | 1'922'000 | 64'370'000 | 60'789'000 |
| performance gain | -2.5 % | -0.7 % | 24.9 % | 30.4 % |
Numbers represent FLOPS.
The PowerPC 440 floating-point coprocessor realized as soft-IP and clocked at 200 MHz has a theoretical asymptotic computational performance of 200 MFLOPS. However, it is barely impossible for practical software to unleash this performance due to the inherent overhead of load/store operations, data dependency issues, or the limited availability of FPU registers.
Nevertheless, it was possible in this project, by solely
adhering to the C programming language for software
implementation, to achieve an FPU performance of up to
64 MFLOPS at application level. It's a solid achievement,
however, there might be room for further improvements by using
assembler instructions for the implementation of the fractal
kernel.
Future steps and improvements might involve:
[1] Xilinx Inc., Virtex-5 Family Brochure, Dec 2008
[2] Xilinc Inc., Virtex-5 Website
[3] Xilinc Inc., Xilinx Virtex-5 ML507 FPGA platform
Last updated: 2012/12/30